積 の 微分 例題

繊細 な 子 習い事積の微分公式の頻出問題6問 - 具体例で学ぶ数学. 積の微分公式を使って有名な関数（sinx,cosx,logx,e^x）のかけ算の導関数を計算する例題を6問説明します。 積の微分公式： ${f(x)g(x)}$$=f(x)g(x)+f(x)g(x)$ 「片方微分、片方そ. 積の微分と商の微分 | おいしい数学. HOME. ノート. 積の微分と商の微分. 微分 (数学Ⅲ) (教科書範囲) ★★. 積の微分と商の微分公式について扱います．. 目次. 1： 積の微分と商の微分とその証明. 2： xn x n ( n n は整数)の微分とその証明. 3： 例題と練習問題. 積の微分と商の微分とその証明. (積の微分) {f (x)g(x)}′ = f ′(x)g(x)+f (x)g′(x) { f ( x) g ( x) } ′ = f ′ ( x) g ( x) + f ( x) g ′ ( x) (商の微分). 積の微分公式とその証明の味わい | 高校数学の美しい物語. 積の微分公式を使う例題. 2つの関数 f (x),g (x) f (x),g(x) の積 f (x)g (x) f (x)g(x) の微分は f (x)g (x)+f (x)g (x) f ′(x)g(x)+ f (x)g′(x) で計算できる，というのが積の微分公式です。 例題. x^2sin x x2sinx を微分せよ。 解答. 2つの関数 f (x)=x^2 f (x)= x2 と g (x)=sin x g(x) = sinx の積の微分を計算したい。 x^2 x2 の微分は. f (x)=2x f ′(x) = 2x. sin x sinx の微分は. g (x)=cos x g′(x) = cosx. よって，積の微分公式. 積の微分公式 | 証明, 問題と解き方. 【例題】の解答. 憤怒 の 天使 アクローマ

バイク タイヤ 交換 どこで問題の関数において. 、 とおくと積の微分公式 から、 と解くことができます。 【1-1】積の微分公式の証明. 積の微分公式を 導関数の定義 から導きます。 関数 の 導関数 は、以下の式により定義されます。 【 導関数の定義 】 関数 の導関数. 上記の導関数の定義を使用して、積の微分公式を証明します。 公式の証明は、 の項を加えることにより、 と の定義式を作り出すところがポイントです。 ここで、 であることから、 が導かれます。. 積の微分・商の微分・和の微分の公式 ～ 証明と例題 ～ - 理数 . 積の微分の公式・商の微分の公式・和の微分の公式・定数倍の微分を証明し、幾つかの例を紹介するページです。 積の微分・商の微分・和の微分の公式 ～ 証明と例題 ～ - 理数アラカルト -. 積・商の微分の公式と証明・例題 | 数学の庭. 積・商の微分の公式と証明・例題 | 数学の庭. 極限, 微分 数Ⅲ. 目次. 積・商の微分の公式. 証明：積の微分. 証明：商の微分. 例題. 積・商の微分の公式. 夢 占い 森 の 中 を 歩く

イスマエル の 亡霊 たち関数 f(x), g(x) f ( x), g ( x) が微分可能であるとき, 次が成り立ちます。 積の微分. {f(x)g(x)}′ = f′(x)g(x) + f(x)g′(x) { f ( x) g ( x) } ′ = f ′ ( x) g ( x) + f ( x) g ′ ( x) 商の微分. 【標準】積の微分と商の微分 | なかけんの数学ノート. 例題1. 次の関数を微分しなさい。 [ y= (x-1) (x-2) (x-3) ] 2つの関数の積の微分は、 【基本】積の微分 で見ました。 $f (x)g (x)$ の微分は、 [ f (x)g (x)+f (x)g (x) ]となるのでした。 ただ、今回は3つの関数の積になっています。 この場合は、「2つの関数の積の微分」を繰り返せばいいんですね。 $f (x)= (x-1)$, $g (x)= (x-2) (x-3)$ とすれば、微分した結果は $f (x)g (x)+f (x)g (x)$ となります。 ここで、 $g (x)$ が出てきますが、ここでまた「2つの関数の積の微分」の公式を使えばいいわけですね。. 積の微分 公式と証明 覚え方も | 高校数学の知識庫. 数学3の微分でまず覚えておきたいのがこの「積の微分」の公式。 これを知らないと微分ができないと言っても過言ではないです。 微分をする対象となる関数は単純な一つの関数で表されるだけではないですよね。 例えば. y = sin x cos x. こんな関数。 これは sin や cos 単体なら微分することが可能なことは後々わかりますが、 このように掛け算になっていると太刀打ちできません 。 もちろんこれだけではなく、 y = ( x + 2) ( 2 x + 3) こんなのも普通には微分できないですね。 数学Ⅱの範囲ではこういう場合、 展開してから微分するのがお馴染み でした。 ですが見方を変えればこれは. ( x + 2) と ( 2 x + 3) の掛け算. ですよね。. 【基本】積の微分 | なかけんの数学ノート. 積の微分. 関数 f ( x), g ( x) が微分可能であるとき、次が成り立つ。 { f ( x) g ( x) } ′ = f ′ ( x) g ( x) + f ( x) g ′ ( x) 例えば、 y = ( x 3 + 1) ( x 4 − 1) の微分を計算してみましょう。 今までなら、まずは展開しないと微分できませんでした。 展開すると. y = x 7 + x 4 − x 3 − 1 となります。 これを微分して y ′ = 7 x 6 + 4 x 3 − 3 x 2 となります。 これを、積の微分を使って計算しなおしてみましょう。 y = ( x 3 + 1) ( x 4 − 1) を微分すると. 積の微分公式と商の微分公式 | 理数系学習サイト kori. まず、積の微分公式の具体的な計算の例をいくつか見てみます。 積の微分公式を使った計算例. y＝sinx cosx 【2つの 三角関数 の積】の微分は次のようになります。 d dx{(sin x)(cos x)} = (sin x)′(cos x) + (sin x)(cos x)′ =cos2 x −sin2 x. 加法定理 を考えると、この結果はcos 2x に等しくなります。 sin x cos x= (sin 2x)／2 として、xで微分した時の結果と一致します。 （この時、合成関数の微分公式を使用しているので注意。 y＝sin 2 x の微分を考えます。 これに積の微分公式を適用する場合にはy＝ (sin x)・ (sin x)と考えるわけです。. 積の微分. 積の微分. 大きな区分. 高校数学 >> 高校数学Ⅲ >> 微分. 現在地 と前後の項目. 積の導関数 / 商,分数関数の導関数 / 合成関数の導関数 / 媒介変数表示の導関数 / 無理関数と分数指数 (復習) / 無理関数の導関数 / 陰関数の導関数 / 重要な極限値 (sinx/x) / 三角関数の導関数1 / 三角関数の導関数2 / 指数，対数関数の導関数 / 対数微分法 / いろいろな関数の導関数 / 極大値，極小値 / 漸近線の方程式1 / 漸近線の方程式2 / 凹凸と変曲点 / 増減.極値/凹凸.変曲点/漸近線/グラフ (1) / 分数関数の漸近線/グラフ (2) / グラフの概形と漸近線（一覧） / 媒介変数表示…接線.法線.速度 / 媒介変数表示とx,y方向の変化 /. 【教科書レベルの問題一覧と解答】数学Ⅱ｜微分と積分 | 教科 . このページは「高校数学Ⅱ：微分と積分」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう! また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使える. 【積の微分公式】5分でok!証明と覚え方をわかりやすく解説 . 積の微分公式. 2つの関数 f(x), g(x) の積 f(x)g(x) の微分は、次のようになります。 ポイント. f(x), g(x) が微分可能なとき、 {f(x)g(x)}′ = f′(x)g(x) + f(x)g′(x) 覚え方のコツは、 微分そのまま＋そのまま微分. です。 例題. (x2 + 1) sin x を微分せよ。. 高校数学の微分公式一覧（例題と証明付き） | 理系ラボ. 1. 高校数学の微分公式一覧. 1.1 微分の記法. まずは微分の記法から説明していきます。 微分の記法. (x)の関数(y=f(x))を微分して得られる関数のことを導関数といい. [y^{prime}=frac{d y}{d x}=frac{d}{d x} y=f^{prime}(x)=frac{d f(x)}{d x}=frac{d}{d x} f(x)] などと記されます。 1.2 微分の基本性質・公式. 次に、微分で用いる基本公式を説明します。 証明も後述するのですが、形を覚えることもかなり大切です。 微分基本公式. 基本性質. 項別に微分することができ、定数は外に出すことができる（このことは線形性と呼ばれる）. 【高校数学Ⅲ】「和・差・積の微分公式」(問題編2) | 映像授業 . POINT. 積の微分は， (前の微分)× (後ろそのまま)+ (前そのまま)× (後ろ微分) で計算できます。 (前の微分)× (後ろそのまま)+ (前そのまま)× (後ろ微分) 積の微分公式 (前の微分)× (後ろそのまま)+ (前そのまま)× (後ろ微分) を活用しましょう。 (前の微分)= (3x 2 -2)=6x， (後ろ微分)= (x 2 +x)=2x+1より，次のように計算できます。 答え. 和・差・積の微分公式. 46. 友達にシェアしよう! 導関数の問題. 商の微分公式. x^pの微分公式. 微分係数f（a） 導関数f（x） 和・差・積の微分公式. 微分法の問題. 導関数. いろいろな関数の導関数. 高校数学Ⅲの問題. 複素数平面. 式と曲線. 梅 の 木 庭 風水

修了 検定 落ち た お金種々の関数. 極限. 微分の基本計算（積の微分・商の微分・合成関数の微分の適用 . 例題1 積の微分を使う. 次の関数を微分せよ。 (1) x2 logx (2) ex sinx. 答え (1) 積の微分より. (x2)′ logx +x2(logx)′ = 2x logx +x2 ⋅ 1 x = 2x logx + x. (2) 積の微分より. (ex)′ sinx +ex(sinx)′ = ex sinx +ex cosx. 例題2 商の微分を使う. 次の関数を微分せよ。 (1) 1 xn (2) tanx (3) 2x x2 + 4. 答え (1)商の微分より. 0 ⋅xn − 1 ⋅ nxn−1 (xn)2 = −n 1 xn+1. (2) tanx = sinx cosxとして商の微分 より. 男の子 の ツム で コイン を 680 枚

お 食い初め 歯 固め の 石 ない【教科書レベルの基本計算問題一覧と解答】数学Ⅲ｜微分法 . 【問題一覧】数学Ⅲ：微分法. 微分法の基本性質. 無理関数と分数関数の微分. 曲線の方程式の微分. 媒介変数表示の微分. 三角関数の微分. 対数関数の微分. 対数微分法. 指数関数の微分. 【問題一覧】数学Ⅲ：微分法. 微分法の基本性質. 問題 次の関数を微分せよ。 (1) y = x5 − 2x4 + 5x3. (2) y = (x2 + 1)(3x − 2) (3) y = x2 x − 1. (4) y = (2x − 3)3. (5) y = 1 (2x − 3)2. [ 解答を見る ] 無理関数と分数関数の微分. 問題 次の関数を微分せよ。 (1) y = x 23. (2) y = x5−−√3. (3) y = 1 x x−−√. 定積分で表された関数の微分の公式 | 高校数学の美しい物語. 耳鳴り 頭 が ぼーっと する

くじ め 屋 中津このページでは，定積分で表された関数の微分公式の証明，例題，より一般的な公式について解説します。 目次. 公式の証明. 簡単な例題.

より一般的な公式. 公式の証明. 定積分の（高校数学における）定義をきちんと理解していれば証明は難しくありません。 証明. f (x) f (x) の原始関数の1つを F (x) F (x) とおく。 つまり F (x)=f (x) F ′(x) = f (x) である。 このとき，定積分の定義（→注意）より， displaystyleint_a^xf (t)dt=F (x)-F (a) ∫ ax f (t)dt = F (x)−F (a) なので，これを x x で微分すると F (x)-0=f (x) F ′(x)−0 = f (x) となる。. 合成関数の微分・積の微分・商の微分：公式と証明 | k-san.link. 【この記事の概要】 合成関数の微分法，積の微分法，商の微分法について，公式とその証明を示します．. 導関数の定義と連続関数の定義を用います．商の微分は，合成関数の微分と積の微分を組み合わせることで導くことができます．. 【スマホでの数式表示について】 当サイトをスマートフォンなど画面幅が狭いデバイスで閲覧すると，数式が画面幅に収まりきらず，正確に表示されない場合があります．その際は画面を回転させ横長表示にするか，ブラウザの表示設定を「PCサイト」にした上でご利用ください．. 合成関数の微分・積の微分・商の微分の公式. 合成関数の微分法 (derivative of a composite function あるいは chain rule)として， (1) あるいは. (2). PDF 微分と積分 - 【高校数学】例題＆問題集. 微分と積分. Math-Aquarium【例題】微分と積分 1 Ox. f (b) . y. ba. B A. 子宮 筋腫 の ツボ

時間 を 数値 に 変換y＝f(x) f (a) 微分と積分. 1平均変化率と微分係数 関数f(x)＝x2－4xについて，次のものを求めよ。 (1)xの値が1 から4 まで変化するときの平均変化率 (2)x＝3 における微分係数 (3) 曲線y＝f (x) 上の点A(t，f(t)) における接線の傾きが1 になるときの，tの値. 要点.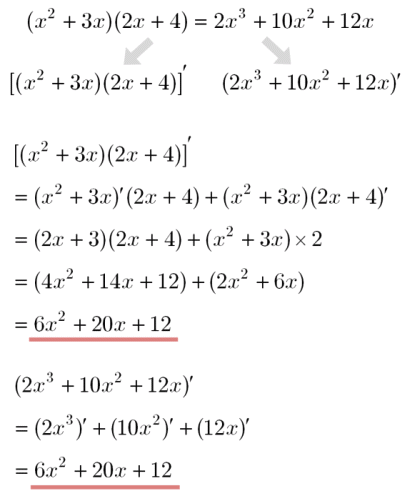

平均変化率 関数y＝f(x) において，xの値がaからbまで変化するとき， xの変化量はb－a，yの変化量はf(b)－f(a)であり， このときの変化の割合 . ① を，xの値がaからbまで変化するときの関数f(x)の 平均変化率 という。. 演習問題（微分積分）｜熊本大学数理科学総合教育センター. 熊本大学 大学教育統括管理運営機構附属 数理科学総合教育センター／Mathematical Science Education Center 〒860-8555 熊本市中央区黒髪2-40-1 全学教育棟A棟3階 096-342-2771（数理科学総合教育センター事務室） E-mail . 分数関数の微分公式(商の微分)とその証明・計算例 | 高校数学の . 分数関数の微分の練習問題. そもそも分数関数とは？ 分数関数とは，以下のような分数で表される関数です。 分数関数の例. y=dfrac {1} {x} y = x1 y=dfrac {4x^2} {x^4+3x^2+x-1} y = x4 +3x2 +x −14x2 y=dfrac {1-sin theta} {cos^2 theta} y = cos2θ1−sinθ. 分子を表す関数を f (x) f (x) ，分母を表す関数を g (x) g(x) とおくと，分数関数は dfrac {f (x)} {g (x)} g(x)f (x) のように表すことができます。 分数関数の微分公式. 令和の一橋後期数学 -2024年- - ちょぴん先生の数学部屋. 先日行われた2024年度の一橋大学の後期数学を解いてみました。 ※一橋の後期は文系向けにも関わらず数Ⅲが出題範囲に含まれています。なので、どうしても数Ⅲの知識が不可避な問題については「※数Ⅲ必須」とコメントを付けておきます。. PDF 微分と積分 - 【高校数学】例題＆問題集. 解答. 求める平均変化率は. 求める微分係数は. 点 における接線の傾きが であるから = よって. したがって . 2. 関数f (x)=x2+3x を,定義に従って微分せよ。 解答. 3. 次の関数を微分せよ。 y=x3-3x2-3x-6. y=(x+2)(x-4)2. 解答. y=(x3-3x2-3x-6)=(x3)-3(x2)-3(x)-(6)=3x2-3・2x-3・1-0=3x2-6x-3. y=(x+2)(x-4)2=(x+2)(x2-8x+16)=x3-8x2+16x+2x2-16x+32=x3-6x2+32であるから. y=(x3-6x2+32)=(x3)-6(x2)+(32)=3x2-6・2x+0=3x2-12x. 4. PDF 2024年度 生命医科学部 医情報学科 開講科目一覧表. 「人体の構造と機能Ⅱ」を登録中もしくは登録した経歴があること。3～ 先行登録科目である。『登録要領』を参照すること 2012年度生以降対象 「人体の構造と機能Ⅰ」を登録中もしくは登録した経歴があること。2～ 説明会や選考を行う。. PDF 農学部の学位授与方針（Dp） 地域環境工学科の学習・教育 . 授業科目の再編について. 農学部の学位授与方針(DP) 生命・食料・環境に関する世界. 水準の自然科学・社会科学研究. の理解力. 生命・食料・環境に関して人類が. 直面する課題を科学的に解決す. る構想力. 生命・食料・環境に関連する産. 微分とは？微分のやり方と全公式をわかりやすく解説! | 受験辞典. 抹茶 蚕 の ふん

資本 金 の 払込 証明 書この記事では、「微分」とは何かをわかりやすく解説していきます。 微分のやり方や、高校で習う微分公式を例題付きで解説していきますので、この記事を通してぜひマスターしてくださいね。 目次微分とは？微分の記号微分のやり方① . 微分公式一覧（基礎から発展まで） | 高校数学の美しい物語. 積の微分公式とその証明の味わい . 商の微分公式をわかりやすく【例題・証明・覚え方】 人気記事 平均値，中央値，最頻値の求め方といくつかの例 .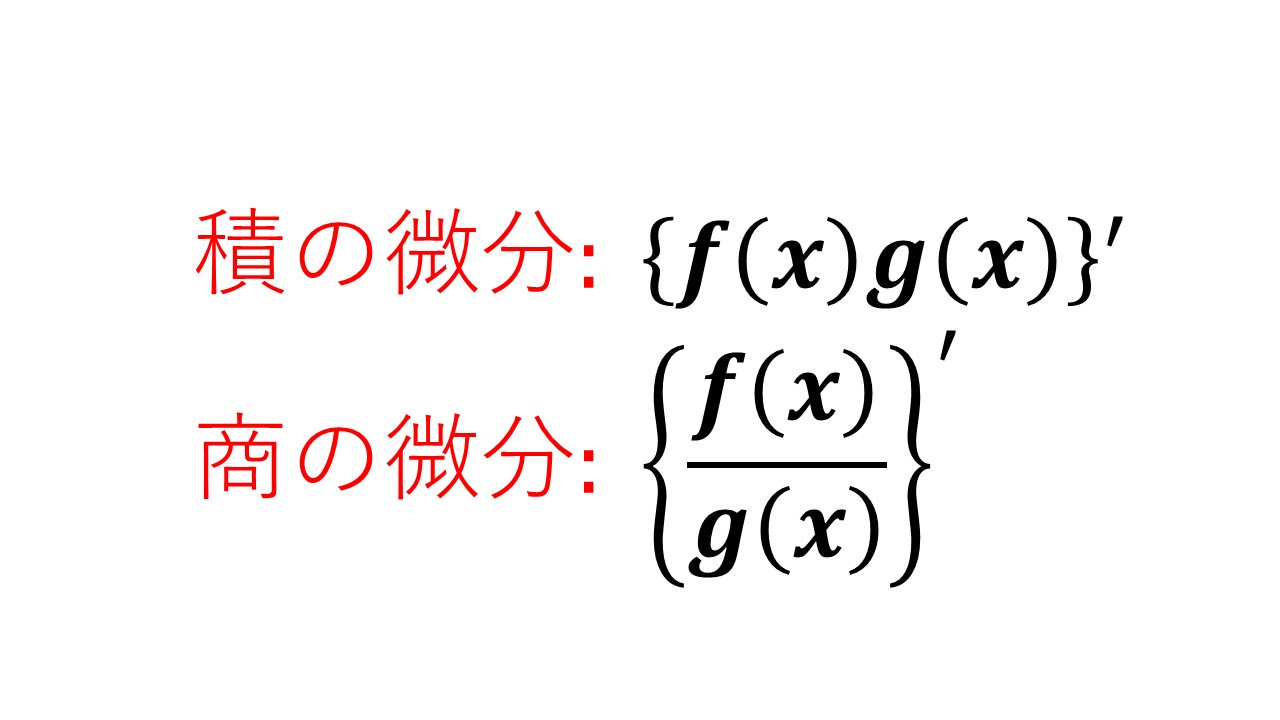

共分散の意味と簡単な求め方 . 部分分数分解の3通りの方法 . 部分積分 | おいしい数学. 部分積分とは，2つの関数の積で構成された関数を積分する手段です． $displaystyle int_{}^{} x sin x,dx$ 上のような積分は，(微分は簡単ですが)積分をするのは難しく，それ用の公式が必要になります．. うさぎでもわかる解析 Part14 偏微分（偏導関数・偏微分係数の計算方法） | 工業大学生ももやまのうさぎ塾. 偏微分は微分する以外のものを定数とするということがわかればそこまで難しくはないことがわかりますね。 また、数3などの微積が苦手な人は特に計算練習をしておくとこれから先の解析学の単元においてもスムーズに勉強できるかと思います。. 内積と外積の時間微分 - ぽこラボ勉強ブログ. 内積と外積の時間微分. Shocho 2019年9月20日. (※数式が見切れている場合は横スクロールしてください。. 流れ的には外積の微分だけ見ておけば十分ではあるのですが、ついでに内積の微分もみておきたいと思います。. ベクトルの微分も習いましたし、積の形 . 分数関数の微分（商の微分公式） - 具体例で学ぶ数学. 商の微分公式について. ～覚え方～. 分母は2乗するだけなので覚えやすいですが、分子がやや複雑で覚えにくいです。. 「分子 f ( x) を先に微分」と覚えましょう。. ～分子が1の場合～. 分子が 1 の場合が頻出です：. 1 f ( x) の微分は、 − f ′ ( x) f ( x) 2 と . y=xe^xの微分、積分、グラフなど - 具体例で学ぶ数学. 江戸川 乱歩 緑 衣 の 鬼

頭痛 に 効く 飲み物 コンビニy=xe^xの微分は積の微分公式を使います。極限の計算方法も解説します。次に、これらの結果を使ってy=xe^xのグラフを書いてみます。 . 積の微分公式を使う最も典型的な例題です。→積の微分公式の頻出問題6問 . 絶対値を含む関数の微分 | 教えて数学理科. 絶対値を含む関数のグラフや極値に関する問題について見ていきます。基本は絶対値の中身の正負で場合分けになりますが、3次以上の関数のときは(x)軸との交点が容易に求まらない(場合分けの境目が具体的に求まらない)ケースもあります。(例題)(1. 【指数関数の微分】公式の証明から例題まで解説｜高校生向け受験応援メディア「受験のミカタ」. 指数関数の微分の例題. 以上が指数関数のごく基本的な形をしたものの微分についてでしたが、 これにさらにどこかに数がくっついたときの計算 もできるようにしましょう。大学入試などでは必ずそのような変化のある式を微分する必要を迫られます。. 【標準】指数関数・対数関数の微分 | なかけんの数学ノート. 指数関数の微分. 【基本】指数関数の微分 で見た通り、一番重要な微分の式は、 ( e x) ′ = e x です。. 底が e でないときは、この場合も変換してから考えたほうがいいでしょう。. これを踏まえて、次の問題を考えてみます。. 例題2. 次の関数を微分しなさい . うさぎでもわかる解析 Part02 逆三角関数 | 工業大学生ももやまのうさぎ塾. うさぎでもわかる解析 Part02 逆三角関数. 2019年6月20日 2021年7月16日 34分53秒. ももうさ. スポンサードリンク. こんにちは、ももやまです。. 今回は解析の前半で習う逆三角関数についてまとめました。. 前回のロピタルの定理と同様、演習問題が若干多めです . ベクトル・行列を含む微分 - TauStation. 積の微分 行列の積のスカラーによる微分 (18) これは素直に次のように確認できる。 (19) 一次～二次形式の微分 Axの形式. ベクトルAxをベクトルxで微分するのにの考え方で計算する。 ベクトルxをn次、行列Aをm×nとすると、ベクトルAx次数はm次となる。. 逆関数とは？逆関数の求め方や微分積分をわかりやすく解説 | 受験辞典. この記事では、「逆関数」の意味や求め方を、豊富な計算問題を通してわかりやすく解説します。 また、逆関数の微分・積分の公式についても説明しますので、この記事を通してぜひマスターしてくださいね! 目次逆関数とは？【復習】 . ライプニッツの公式の証明と二項定理 | 高校数学の美しい物語. 積の微分を効率よく行うためのライプニッツの公式と二項定理，多項定理との関係を紹介します。 . 数学的帰納法をわかりやすく【例題3問、応用5パターン】 マクローリン展開 . バーゼル問題の初等的な証明 . 原始多項式とその積について . べき関数（y=x^n . 積の微分法則 - Wikipedia. 標準的な微分積分学の場合. 積の法則の厳密な証明には、 微分の定義 と 極限の基本性質 を用いる。. 積 h(x) = f(x)g(x) について、各因子 f, g は一点 x0 においてそれぞれ微分可能であるものとする（以降、本節を通して x0 は固定するものとする）。. 主張は . 人生 を 四季 に 例える

鶯谷 ち じ ょ逆関数の微分 | おいしい数学. 逆関数の微分公式とその証明. 微分可能な関数 y = f (x) y = f ( x) の 逆関数 y = g(x) y = g ( x) が存在するとする． b = f (a) b = f ( a) とし， f ′(a) ≠ 0 f ′ ( a) ≠ 0 ならば. y = g(x) y = g ( x) 上の (b,a) ( b, a) での接線の傾きは， y = f (x) y = f ( x) 上の (a,b) ( a, b) での接線の . 【数学Ⅲ】積分計算の型網羅part5(三角関数） - 理系ラボ. 数学Ⅲ2019.08.21. 【数学Ⅲ】積分計算の型網羅part5(三角関数）. 東大塾長の山田です。. このページでは、三角関数の積分について詳しく説明しています!. 基本公式と基本方針を基にして、様々な例題や、発展的な公式について詳しく説明しています。. この . 三乗根、累乗根の微分 - 具体例で学ぶ数学. 公式の覚え方、具体例. 累乗根の微分は、まず、累乗根を xα という形に直した上で、 指数部分を前に出して、指数部分は 1 を引く とおぼえましょう。. 例えば、 x の三乗根 x−−√3 は x1 3 と直せて、その微分は. 13x1 3−1 = 13x−2 3. となります。. 例題： x の . うさぎでもわかる複素解析 Part2 複素関数の微分可能性とコーシー・リーマンの関係式 | 工業大学生ももやまのうさぎ塾. 2次正方行列のサラスでは、赤色方向（左上→右下）の積から青色方向（左下→右上）の積の値を引きますね。 サラスの公式の引く方向に対してマイナスが付く と考えるとコーシー・リーマンの公式でどっちにマイナスが来るかを覚えることができます。. うさぎでもわかる解析 Part15 合成関数の偏微分 | 工業大学生ももやまのうさぎ塾. うさぎでもわかる解析 Part15 合成関数の偏微分. こんにちは、ももやまです。. 今回は合成関数の偏微分についてまとめていきたいと思います。. 前回の記事（Part14 偏微分）はこちら!. （偏微分がよくわかっていない人はこちらで復習をしてからご覧になる . ライプニッツの公式 ～具体例と証明～ - 理数アラカルト. 関数の積のn階微分を求めるライプニッツの公式 (Leibniz-rule) を具体例を挙げながら、丁寧に証明するページです。二項分布との類似性や差分商に対するライプニッツの公式も書かれています。. 【基本】定積分の部分積分 | なかけんの数学ノート. 部分積分を使った定積分の計算その1. 例題1. 次の定積分を計算しなさい。. ∫ 0 π x sin x d x. 直接不定積分を求めることが難しく、置換積分も難しそうな場合に、部分積分が使えることがあります。. 被積分関数が2つの関数の積になっていて、片方は微分する . 複素微分を具体例とともに解説!正則関数の重要定理も紹介! - あーるえぬ. 例4（複素共役を返す関数）. 複素関数 f 4: C → C を f 4 ( z) = z ― で定める． f 4 が微分可能な点を求めよ．.

f 4 は複素共役を返す複素関数ですね．結論を先に言えば，この f 4 も C 上の全ての点で 微分不可能 です．. 任意に α = p + q i （ p, q ∈ R ）をとる．. [1 . 対数微分法 | おいしい数学. 対数微分法の手順. STEP1：両辺の絶対値をとって (正であることが保証されているならば不要)，自然対数をとる．. STEP2：両辺 x x で微分する．. STEP3：両辺に y y をかけて整理して終わり．. 対数をとるときに，真数条件のことを考慮しないといけないので . 高校数学Ⅲ 微分法（基本計算パターン） - 受験の月. 当カテゴリでは、高校数学の最重要分野「微分・積分」のうち、微分法の基本計算および頻出のグラフの図示のパターンを網羅する。 微分・積分は大学数学の柱であり、多くの大学の2 次記述試験では数Ⅲの微分・積分の問題が5 割近くを占める。. ベクトルの微分 | 高校数学の美しい物語 - 学びTimes. 「ベクトルの微分」「ベクトルで微分」について，以下の3種類の意味と関連する公式を紹介します。 . →勾配ベクトルの意味と例題. 積の微分公式とその証明の味わい . マクスウェル方程式 . 人気記事. ベクトル関数の微分 - 単位の密林. ベクトル関数 の微分計算は 各成分を微分するだけ でよい。. すなわち. 例えば、先ほどの ベクトル関数 を変数 について微分すると. となる。. ベクトル関数 の2回以上の微分についても同様に各成分関数を微分するだけでよい。.

つまり、. 三角関数の微分公式と問題例 | 高校数学の美しい物語. 三角関数を含む関数の微分では「合成関数の微分」「積の微分」「商の微分」を使うことが多いです。 忘れた方は以下の記事を参照ください。 合成関数の微分についてはこちら →合成関数の微分公式と例題7問. うさぎでもわかる解析 Part16 全微分（全微分可能性の判定法・全微分の応用） | 工業大学生ももやまのうさぎ塾. 1．全微分とは まず、全微分とはどんなものなのかを簡単に説明したいと思います。 2変数関数 ( z = f(x,y) ) の ( x ) こんにちは、ももやまです。 今回は全微分についてです。 1．全微分とは まず、全微分とはどんなものなのかを簡単に説明したいと思い . 偏微分とは～定義と例題と図形的意味～ - 数学の景色. 多変数関数に関して，ある1変数のみを変数とみて，残りの変数を定数と見たときの微分を偏微分と言います。本記事では，偏微分の定義・例題・図形的意味について，まず2変数関数の場合を考え，それからn変数関数の場合を解説しましょう。. 合成関数の微分法（問題と答え）【微分計算（数学Ⅲ）をマスターしよう】 | 大学受験の王道. 積の微分を利用する。 loguを全体、2x+3を中身と考える。 ③. 積の微分を利用する。 loguを全体、sinxを中身と考える。 ④. 商の微分を利用する。 sinuを全体、cosxを中身と考える。 e u を全体、3x+1を中身と考える。 ⑤. 合成関数の微分を2回利用する。. 【基本】合成関数の微分の計算 | なかけんの数学ノート. ここでは、合成関数の微分の計算例をいくつか見ていきます。積の微分と合成関数の微分例題1次の関数を微分しなさい。 [ y=(x^3+x^2+1)^3 ]これは、【基本】積の微分で見た内容を使い、 $(x^3+x^2+1). 積の導関数公式と証明を解説｜例題あり | 数学のトムラボ. 今回は関数の積を微分する公式について解説します。具体的には積の導関数公式とは何かの説明、次に証明して、最後に使い方を解説していきます! 積の導関数公式とは 積の導関数公式とは、関数の積を微分する公式です。公式は下記のように表されます。 $$. 定積分で表された関数の微分 | おいしい数学. 定積分で表された関数の微分の解き方. f (x) = ∫ x 1 (t2 −t)dt f ( x) = ∫ 1 x ( t 2 − t) d t ⋯ ⋯ ①. 上の関数で f ′(x) f ′ ( x) を求めたいとき， f (x) f ( x) の正体を積分計算して出してから微分してもいいですが，わざわざ積分して微分するのは面倒な感じがし . 不定積分の意味・公式・例題 | 高校数学の美しい物語. 積分定数. 例題1で見たように，不定積分の答えは (関数)+ (任意の定数) という形になります。. 定数を微分しても 0 0 なので微分した結果に影響を与えないからです。. この任意の定数のことを 積分定数 と言います。. 例題1の答えは. x^2+C: x2 + C (ただし C C は . 指数，対数関数の微分 | おいしい数学. 指数，対数関数の微分公式とeの定義を扱います．例題と練習問題を厳選． 指数，対数関数の微分公式とeの定義を扱います．例題と練習問題を厳選． . 上の公式を使いますが，積の微分 . うさぎでもわかる微分方程式 Part14 ラプラス変換のいろは | 工業大学生ももやまのうさぎ塾. うさぎでもわかる微分方程式 Part14 ラプラス変換のいろは. 2020年5月1日 2023年4月19日 62分17秒. ももうさ. スポンサードリンク. こんにちは、ももやまです。. 今回は、ラプラス変換を用いた微分方程式について説明する前に、ラプラス変換とはどのようなものな . 部分積分を使う積分計算の解き方 - 例題と解説. このページでは、上に示した4つの積分計算を例題として、部分積分法の使い方を解説しています。 部分積分の公式の導出と、使い方の詳しい説明は前ページ「部分積分の公式とその証明方法、使い方のコツ」をご覧ください。. 自然対数関数の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ. 自然対数関数の微分. 関数 が 自然対数関数 であるものとします。. つまり、 はそれぞれの に対して、 を定めるということです。. が定義域上の点 を含め周辺の任意の点において定義されている場合、点 において 微分可能 であるか検討できますが、 は点 . 【高校数学Ⅱ】「関数の微分公式」(例題編) | 映像授業のTry IT (トライイット). Try IT（トライイット）の関数の微分公式の例題の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の . xsinxの微分、グラフ、積分など - 具体例で学ぶ数学. xsinxの微分は積の微分公式を使います。 グラフの概形はy=xとy=-xの間を振動するので図のようになります。 xsinxの積分には部分積分を使います。. 部分積分法 ~積（掛け算）の積分公式~ の使い方と解説 | Headboost. 部分積分法は、関数の積を積分したいときに使う公式です。そして、積分は微分の逆演算であるため、部分積分法は積の微分公式の逆演算ということになります。 このページでは、この部分積分法について詳しく解説していきます。. フーリエ変換の意味と応用例 | 高校数学の美しい物語. 話しかける な オーラ 診断

フーリエ変換とは. フーリエ級数展開 とは，周期関数を三角関数（or 複素指数関数）の和で表すというものでした（→ フーリエ級数展開の公式と意味 ， 複素数型のフーリエ級数展開とその導出 ）。. 具体的には，周期 2 k pi 2kπ の関数 f (x) f (x) で適切な . 全微分の考え方とその応用 | 理数系学習サイト kori. 積の形の関数に対する全微分については、通常の1変数関数の場合の、積に関する微分公式同様の式が成立します。 これは数学の解析学ではそれほど重要な式ではありませんが、物理では使う事があるので述べておきましょう。.